In many cases, critical values are required.

A critical value often represents a rejection region cut-off value for a hypothesis test – also called a zc value for a confidence interval.

For confidence intervals and two-tailed z-tests, you can use the zTable to determine the critical values (zc).

Example

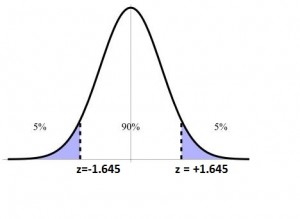
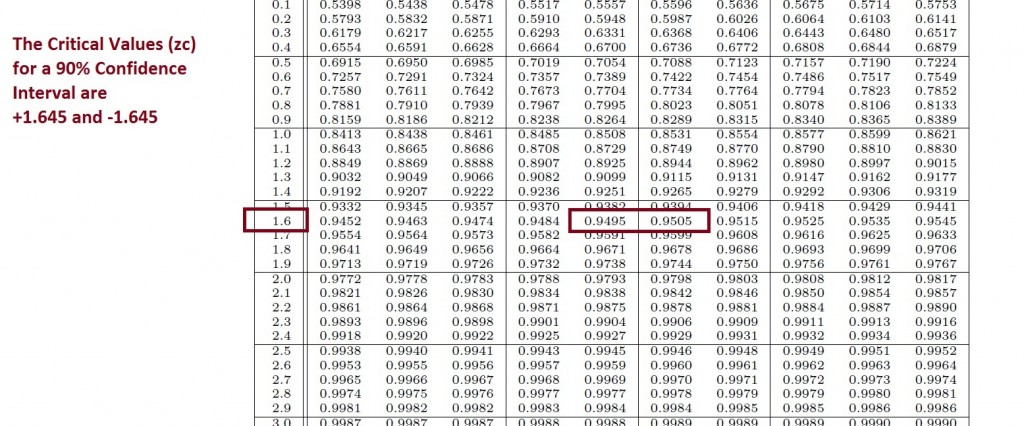
Find the critical values for a 90% Confidence Interval.

NOTICE: A 90% Confidence Interval will have the same critical values (rejection regions) as a two-tailed z test with alpha = .10.

The Critical Values for a 90% confidence or alpha = .10 are +/- 1.645.

Example 2
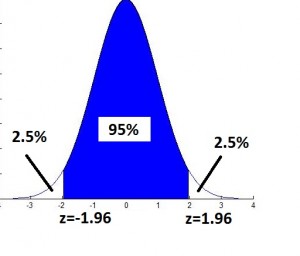
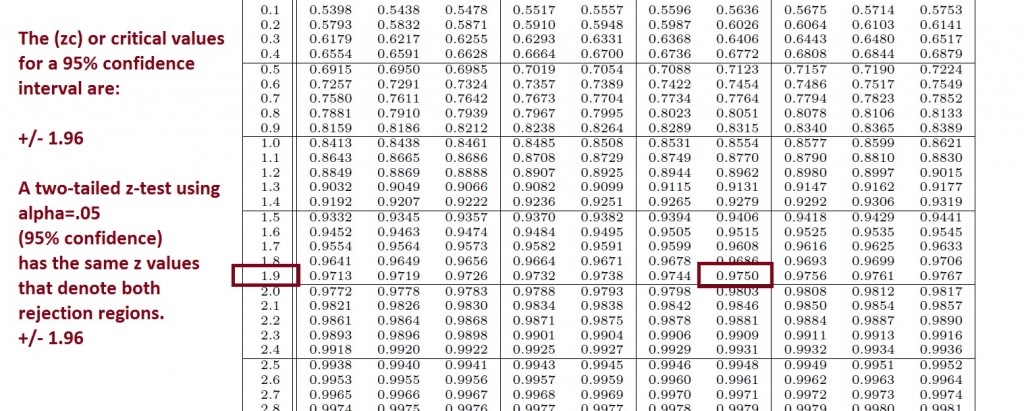
Find the critical values for a 95% confidence interval. These are the same as the rejection region z-value cut-offs for a two-tailed z test with alpha = .05.

Note that when alpha = .05 we are using a 95% confidence interval.